Exemplo 1: Calculando √7921
Passo 1: Valor inicial (estimativa de uma possível raiz)
Tomando 81 como valor inicial, assim w = 81 .
81²=81·81=6561
Passo 2: Cálculo da diferença d:
7921-6561=1360
Passo 3 : Aproximação da constante k:
| d | : w : 2 = | 1360 | : 81 : 2 ≅ 8,4
Passo 4: Determinação da constante k
Divisor de 1360 mais próximo de 8,4 é? k=8
Passo 5: Utilização da fórmula

Passo 6: Teste
89²=89·89=7921
Assim definimos que √7921 = 89
Exemplo 2: Calcule √450241.
Resultado entre 600 e 700, pois
Resultado dentre 600 e ta00, pois 600²=360000 e 700²=490000.
Com unidade 1 ou 9 devido a unidade um do radicando 450241.
Passo 1: Valor inicial (estimativa de uma possível raiz)
Tomando 689 como valor inicial, assim w = 689
689²=689·689=474721
Passo 2: Cálculo da diferença d:
474721 – 450241 = 24480 = d
Passo 3: Aproximação da constante k
| d | : w : 2 = 24480 : 689 : 2
Aproximando os resultados
25000 : 700 : 2 ≅ 17,8
Passo 4: Determinação da constante k
Divisor de 24480 mais próximo de 17,8 é? k = 18
Passo 5: Utilização da fórmula
#include
#include
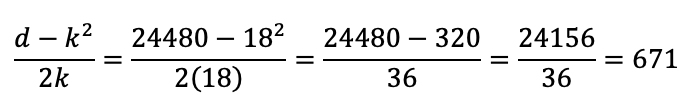
Passo 6: Teste
671²=671·671=450241
Assim definimos que √450241 = 671
Exemplo 3: Calculando √7070281
Resultado entre 2000 e 3000, pois 2000²=4000000 e 3000²=9000000.
Com unidade 1 ou 9 devido a unidade um do radicando 7070281.
Passo 1: Valor inicial (estimativa de uma possível raiz)
Tomando 2681 como valor inicial, assim w = 2681 .
2681²=2681·2681=7187761
Passo 2: Cálculo da diferença d:
7187761 – 7070281 = 117480 = d
Passo 3: Aproximação da constante k
| d | : w : 2 = 117480 : 2681 : 2
Aproximando os resultados
117000 : 2600 : 2 ≅ 22,5
Passo 4: Determinação da constante k
Divisor de 117480 mais próximo de 22,5 é? k=22
Passo 5: Utilização da fórmula
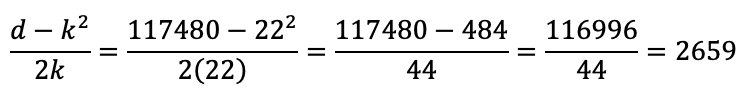
Passo 6: Teste
2659²=2659·2659=7070281
Assim definimos que √7070281 = 2659.
Exemplo 4: Calcule √955551744.
Resultado entre 30000 e 40000, pois 30000²=900000000 e 40000²=1600000000.
Unidade 2 ou 8.
Passo 1: Valor inicial w = 30922, logo 30922²=30922·30922=956170084.
Passo 2: Cálculo da diferença.
d=956170084-955551744=618340
Passo 3: Aproximação da constante.
ΙdΙ:w:2=618340:30922:2
Aproximando os resultados para uma facilitação dos cálculos temos:
618000:30900:2=10
Passo 4: Número divisor de 618340 próximo ou igual a 10.?Assim k = 10
Passo 5: Utilização da fórmula

Logo como 30912²=955551744, temos que √955551744=30912.