²²Calculando-se √L tomando w como como possível raiz o produto inicial será w·w=w², assim temos três hipóteses diferentes:
Hipótese 1: w²=L, logo √L=w
Hipótese 2: w²<L
Processo 1
w²+(w)+(w+1)
w²+2w+1
(w+1)²
Foi somado ao quadrado do valor inicial w² o termo 2w+1.
Processo 2
(w+1)²+(w+1)+(w+2)
w²+2w+1+2w+3
w²+4w+4
(w+2)²
Foi somado ao termo anterior o termo 2w+3.
Processo 3
(w+2)²+(w+2)+(w+3)
w²+4w+4+2w+5
w²+6w+9
(w+3)²
Foi somado ao termo anterior o termo 2w+5.
Processo 4
(w+3)²+(w+3)+(w+4)
w²+6w+9+2w+7
w²+8w+16
(w+4)²
Foi somado ao termo anterior o termo 2w+7.
Processo 5
(w+4)²+(w+4)+(w+5)
w²+8w+16+2w+9
w²+10w+25
(w+5)²
Analisando os termos somados, eles formam uma Progressão Aritmética (2w+1 ,2w+3 ,2w+5 ,2w+7 ,….) de razão 2, primeiro termo 2w+1, como o produto inicial é w², temos que o termo é dado através de sua soma com a soma de termos da Progressão dada, assim temos:
Pela forma geral da sequência dada temos:
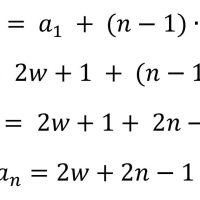
Somando o produto inicial w² com a soma de n termos da sequência temos:
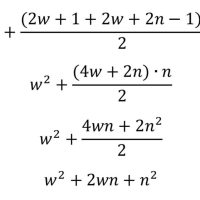
Como mostrado anteriormente a cada processo feito, temos o quadrado de um sucessor de w e consequentemente um sucessor de w é igual a √L, neste fator final podemos definir que w é o número escolhido para o produto inicial e n o numero de processos utilizados. Caso o produto inicial seja maior que o radicando, o processo é análogo que é a terceira hipótese.